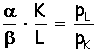Il produttore

La funzione di produzione descrive la tecnologia di un’impresa, in particolare la relazione tra quantità impiegata dei vari fattori di produzione o input e livello del prodotto o output.

Per semplicità consideriamo solo due fattori della produzione: lavoro e capitale.

La funzione di produzione è il massimo prodotto ottenibile dalle diverse combinazioni dei fattori produttivi:

dove L denota la quantità di lavoro impiegato nella produzione, K denota la quantità di capitale e Q la quantità di output.

Una funzione molto usata nell'analisi del comportamento delle imprese (e anche nella teoria del consumatore), è la funzione di Cobb-Douglas :

Fin dal 1928 l'economista americano P.H. Douglas osservando il comportamento delle serie storiche relative al lavoro, al capitale e alla produzione per gli Stati Uniti, in collaborazione con il matematico C.W. Cobb, cercò di interpretare la relazione tra dette grandezze utilizzando la famosa funzione. I due la applicarono con a+b = 1.

La funzione dovrebbe essere più propriamente chiamata "funzione Wicksell", in quanto l'economista svedese Knut Wicksell (1851-1926) introdusse tale tipo di funzioni prima del 1900.

Un modo conveniente di rappresentare graficamente una funzione di produzione è quello di

Ricordiamo che data una funzione z=f(x,y) ,il grafico della funzione nello spazio tridimensionale può essere sezionato con piani orizzontali paralleli al piano xy (z=c); l'intersezione che ne risulta, proiettata sul piano xy è detta curva di livello a quota c di f:

Nella figura sottostante possiamo osservare la rappresentazione tridimensionale e per curve di livello (isoquanti) della funzione di produzione:

Gli isoquanti di produzione rappresentano tutte le possibili combinazioni dell’input L e dell’input K esattamente sufficienti a produrre un dato livello di prodotto Q.

La produttività marginale di un fattore misura l’incremento di prodotto derivante dall’incremento marginale di un fattore, fermo restando l’altro fattore.

Le produttività marginali sono date dalle derivate parziali di Q rispetto ad L e rispetto a K:

Esempio. Consideriamo la funzione di Cobb-Douglas :
La produttività marginale del lavoro risulta:
In particolare, per K=100:
Una prima conclusione è che: La *produttività marginale* dei fattori è positiva: incrementare l’impiego di ciascun fattore comporta cioè un incremento della produzione. Una seconda conclusione è che : La *produttività marginale* dei fattori risulta decrescente (Q’’_LL<0) Vediamolo (per il lavoro) con i numeri:

Come possiamo spiegare un tale andamento decrescente della produttività marginale del lavoro?

Esso significa che la produttività del lavoro diminuisce al crescere dell’uso che facciamo di tale fattore.

Intuitivamente, un’unità addizionale di lavoro (ad esempio un operaio in più) ha maggiore effetto sulla produzione se partiamo da una situazione in cui non vengono usati lavoratori che non se partiamo invece da una situazione in cui vi è già un uso abbondante di lavoratori. Al limite, possiamo trovarci nella situazione in cui un lavoratore in più non ha alcun effetto sulla produzione, o addirittura ha effetti negativi (ad esempio se lo spazio fisico dell’impianto è ristretto).

Anche relativamente alle preferenze del consumatore, si ha che l'utilità marginale dei 2 beni è decrescente. A tal proposito, viene fornito spesso il seguente esempio chiarificatore :

per un assetato, il primo bicchiere d'acqua è molto desiderabile e quindi reca un beneficio elevato. Anche il secondo bicchiere recherà soddisfazione. Dal terzo bicchiere in poi, ogni dose successiva recherà sempre minor soddisfazione fino ad arrivare al punto di creare fastidio. Quindi le dosi (unità) di un determinato bene, soddisfano in modo decrescente il consumatore.

L'elasticità parziale di z rispetto ad x, cioè il numero e_zx, è approssimativamente uguale alla variazione percentuale di z provocata da un aumento dell'1% di x , avendo mantenuto fissa la y (e_z_yha un'interpretazione simile).

Riferendoci ad una funzione di produzione di Cobb-Douglas, il calcolo dell'elasticità porta ad espressioni estremamente semplici (gli esponenti di L e K) ; questa è una delle proprietà di tale funzione che favorisce il suo ampio utilizzo :

Il saggio marginale di sostituzione tecnica SMST (o SST) rappresenta l’inclinazione dell’isoquanto in un punto dato dell’isoquanto stesso (in valore assoluto).

Ci dice in che misura la tecnologia consente di sostituire un fattore all’altro ed è dato dal rapporto tra le produttività marginali:

Per una funzione di Cobb-Douglas, come già visto per il consumatore, ha un'espressione molto semplice:

Nel grafico è rappresentato l'isoquanto corrispondente alla produzione Q=2, relativamente alla funzione:

In questo caso risulta : SMST=K/L.

Osserviamo che nel punto (1,4) la pendenza dell’isoquanto (in valore assoluto) è data da:

.. ed è maggiore che nel punto (4,1), in cui essa ha valore:

Cosa significa per il produttore scegliere in maniera ottimale la combinazione di fattori produttivi?

Il produttore effettua una scelta ottimale quando, nel rispetto dei vincoli di costo, massimizza la produzione e quando minimizza i costi, nel rispetto di un vincolo di produzione.

In termini analitici, quando gli isoquanti sono strettamente convessi (fattori produttivi imperfettamente sostituibili), il punto di ottimo è dato dal punto di tangenza tra vincolo di costo e curva isoquanto , nel primo caso, e vincolo di produzione e curva isocosto, nel secondo. In entrambi i casi, si determina risolvendo il sistema costituito dalle seguenti condizioni:

	1) Condizione di ottimo: pendenza *isoquanto* = pendenza *isocosto*
	nel caso di una Cobb-Douglas :
	2)Vincolo di costo
	1) Condizione di ottimo: pendenza *isoquanto* = pendenza *isocosto* 2)Vincolo di produzione

Fattori perfetti sostituti

Il SMST in questo caso è costante ed è pari al valore assoluto della pendenza:

SMST= b/a

Nel caso di fattori perfetti sostituti la produttività è positiva e costante per ciascuno dei fattori.

In questo caso i fattori devono essere combinati in proporzioni fisse e la funzione di produzione ha gli isoquanti come quelli rappresentati in figura:

Per ottenere Q=6 servono almeno 3 unità di K e 2 unità di L . Usarne in più di uno solo dei due significherebbe sprecare. Per essere usati in modo efficiente, dovranno sempre stare in una relazione tale per cui: K=3/2L che rappresenta la retta che passa per gli angoli di tutti gli isoquanti e identifica le combinazioni efficienti di capitale e lavoro.

In tal caso il SMST non è definito nel punto d'angolo degli isoquanti. Partendo da una combinazione efficiente, se si aumenta l'utilizzo di uno solo dei fattori, l'output non aumenta: la produttività marginale dei fattori è uguale a zero.

La produttività marginale, come abbiamo visto, misura l’effetto sulla produzione di un incremento (marginale) nell’impiego di un fattore.

I rendimenti di scala descrivono invece l’effetto sull’output di un incremento nell’impiego di tutti i fattori nella stessa proporzione, ovvero di una variazione nella scala di produzione, mantenendo invariato il rapporto tra i fattori impiegati, cioè il rapporto K/L.

Immaginiamo di incrementare le quantità di entrambi gli input di un fattore n>1.

Per una Cobb-Douglas, i rendimenti di scala sono indicati dalla somma a+b. Infatti se incrementiamo il lavoro e il capitale di una quantità b>1, si ha:

1. Funzione di produzione Cobb-Douglas con coefficienti a = b = 1/2, cioè:	Q(2L;2K) = 2Q(L;K) rendimenti costanti
2. Funzione di produzione Cobb-Douglas con coefficienti a = b = 1, cioè: Q(L;K) = LK	Q(2L;2K) = (2L)(2K) = 2²LK > 2LK Q(2L;2K) > 2Q(L;K) rendimenti crescenti
3. Funzione di produzione Cobb-Douglas con coefficienti a = b = 1/3, cioè:	Q(2L;2K)<2Q(L;K) rendimenti decrescenti
4. Funzione di produzione *lineare*: Q(L;K)=50L+10K	Q(2L;2K) = 50(2L)+10(2K) = =2(50L+10K) rendimenti costanti