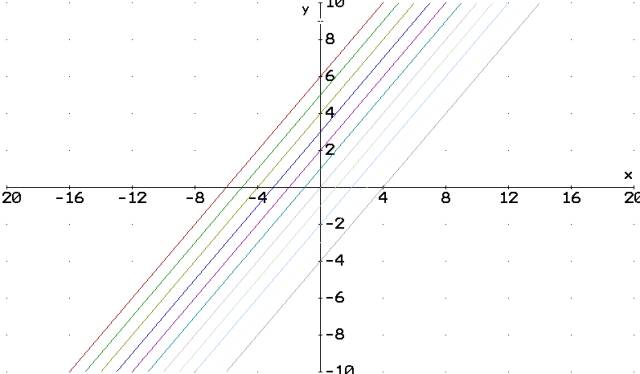
Esercizi pag.442 (Re Fraschini-Grazzi)     “Rappresenta le seguenti funzioni attraverso le linee di livello”

N°184

z=x-y+1     Dobbiamo studiare le intersezioni di questa superficie ( piano ) con i piani  z=k.

                     In pratica si deve sostituire k alla z e studiare la famiglia di curve che si ottiene.

                     Consideriamo k variabile tra  -5 e +5.

K

Retta

-5

y=x+6

-4

y=x+5

-3

y=x+4

-2

y=x+3

-1

y=x+2

0

y=x+1

1

y=x

2

y=x-1

3

y=x-2

4

y=x-3

5

Y=x-4

Metodo “tradizionale”:

             k=x-y+1                  y=x+1-k  (fascio di rette parallele alla 1°bisettrice)

Il grafico in questo caso è molto semplice, in quanto tracciata la prima bisettrice

(y=x), basta tracciare le parallele che incontrano l’asse y nei punti indicati dalle varie ”q”.

 

Con DERIVE :

Author/Expression

Digitiamo la seguente espressione:

Vector(k=x-y+1,k,-5,+5)                   Simplify

Nella finestra  Algebra compariranno tutte le equazioni, già evidenziate; clicchiamo sull’icona che indica il grafico bidimensionale             poi ancora una volta , ed esce il grafico riportato sotto.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


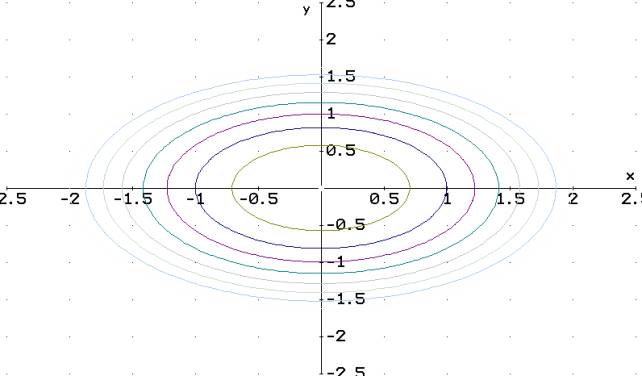
N°185

z=2x2+3y2            z=k    Prendiamo k variabile tra  0 e +8   (Ellissi)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Ripassiamo l’ellisse…..

 

Equazione dell’ellisse in forma canonica

 

 
 

 

 

 

 

 


        

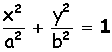
N.B. L’equazione è molto simile a quella di una circonferenza con il centro nell’origine :  x2+y2 = r2

 

Affinché sia un’ellisse è necessario che i coefficienti di  x2  e di  y2 siano diversi (ma ancora entrambi positivi).

N.B. Se   b2 > a2, allora l’asse focale è l’asse  y (l’ellisse risulta più allungata sull’asse y).
 

 

 

 

 

 

Fumetto 4: Come si disegna? 

 


       

 

                                                                              

                                                                           L’ellisse in forma canonica è una curva simmetrica

                                                                            rispetto all’origine.      

 

                    

               Una volta “prelevate” dall’equazione le misure dei  semiassi , a e b , si traccia il rettangolo di

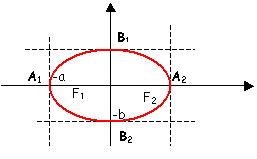               dimensioni  2a e 2b  ,come indicato in figura :      

 

b
 
All’interno del rettangolo si inscriverà 

a
 
l’ellisse (a mano libera).

0
 
 


La curva tocca gli assi nei punti: A1, A2, B1  e B2

detti VERTICI. Risulta :

A1(-a;0)   A2(a;0)   B1(0;b)   B2(0;-b)

 

Se si vogliono calcolare le coordinate dei fuochi , basta  ricordare che :

     F1(-c;0)   ed    F2(c;0)

 

ed anche che :    a2 – c2 = b2                  c2 = a2 - b2                                                           F1,2( ±Ö a2 - b2;0)

 

***************************************************************************

N.B. Se l’asse focale = asse y , cioè se  b2 > a2 , allora il calcolo di  c si esegue invertendo i due

         termini:

                                                  c =  Ö b2 - a2    

         ed i fuochi, essendo sull’asse y, avranno coordinate : F1(0; Ö b2-a2 )  ed    F2(0;-Ö b2-a2 )

Esplosione 1: Esempio***************************************************************************

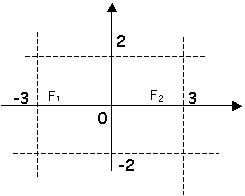
                                 Tracciare il grafico della seguente ellisse e calcolare le coordinate dei fuochi:

                                            

                                           4x2  + 9y2  = 36        

                     ------------------------------------  ---------------------------------

L’equazione non è in forma canonica (a secondo membro ci deve essere 1); dividiamo entrambi i membri per 36   :

                                                                                 

 

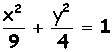
a2 = 9                a = 3  

b2  = 4               b = 2

 


Vertici
 
 A1(-3;0)   A2(3;0) 

  B1(0;2)    B2(0;-2)                

 

Fuochi :

 c = Ö a2 - b2    = Ö 9 – 4   = Ö 5   @ 2,2      F1(-Ö 5 ;0)   F2(Ö 5 ;0)

 

 

 


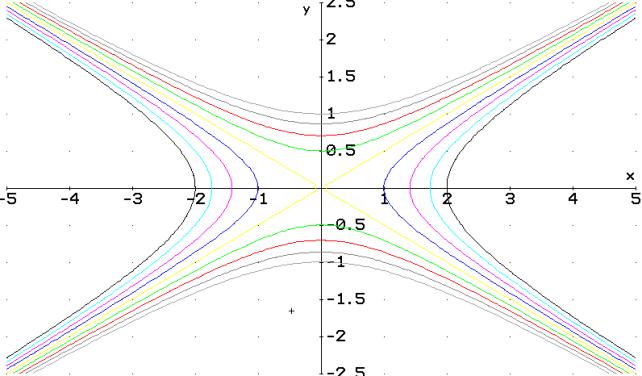
N°186

z=x2-4y2                         Iperboli (Ricordiamo che se z<0 le iperboli hanno asse trasverso l’asse y ; se

                                    z>0 l’asse traverso è l’asse x). Prendiamo  k  tra   –4 e  +4 .