Continuità
Si
potrebbe dire che una funzione è continua se “può essere disegnata senza mai staccare la penna
dal foglio”. Questa definizione, pur se rozza, è sicuramente
efficace e ci permette di affermare con tranquillità che retta e parabola sono
funzioni continue mentre l’iperbole equilatera riferita ai propri asintoti ha
un evidente punto di discontinuità per x=0;
infatti in quel punto si annulla il denominatore e la funzione non esiste:
l’asse delle y è un asintoto
verticale.
La
definizione rigorosa di continuità è la seguente:
ovvero
una funzione è continua in un suo punto x0
se il valore che assume nel punto
è uguale al valore a cui tende in
prossimità del punto x0
.
Una funzione è continua in un
intervallo se è continua in ogni punto dell’intervallo.
Riflessioni sulla definizione di continuità
Affinché la continuità
in un punto sia verificata è necessario che si verifichino le tre seguenti
condizioni:
1.
Esista
2.
Esista finito
3.
Le due quantità (punti 1 e 2) siano uguali.
Funzioni continue
·
Come prima detto, sono sicuramente funzioni continue rette e parabole,
ovvero funzioni razionali intere. Un teorema sul calcolo dei limiti ci permette
di affermare che somma, differenza
e prodotto
di funzioni continue è ancora una funzione continua. Dunque una funzione
razionale intera di grado n (polinomiale
) è una funzione continua.
·
Sono inoltre continue la funzione esponenziale (
)e
la funzione logaritmica(
)
all’interno del campo di esistenza
.
·
Funzioni fratte: la continuità
si interrompe nei punti che annullano il denominatore.
· Funzioni definite a tratti: potrebbe esistere discontinuità nei punti in cui cambia il tratto (punti di confine fra tratti diversi).
Come potremo vedere più avanti potrebbe esistere una continuità parziale, ovvero a destra o a sinistra di un punto.
I punti di discontinuità
vengono classificati di tre specie:
allora si potrebbe avere una
continuità parziale, ovvero a
destra o a sinistra).
tende all’infinito: si
incontra nelle funzioni fratte nei punti che annullano solo il denominatore;
in questo caso la funzione presenta un asintoto verticale di equazione
x=x0
. Si indicano così anche i punti in cui il limite non esiste.
esiste finito ma
o non esiste o assume un valore diverso da quello del limite: si incontra
nelle funzioni fratte nei punti che annullano numeratore e denominatore;
tale tipo di discontinuità viene detto eliminabile in quanto ridefinendo la
funzione può essere eliminata.
1.
Studiare la continuità della funzione
Il
punto a rischio di continuità è x=2 (punto di confine dei tratti).
Possiamo
osservare che
, dunque la funzione esiste
nel
punto x=2. In prossimità del punto si hanno i due seguenti limiti:
(primo tratto) e
(secondo tratto).
Dunque
x=2 è un punto di discontinuità di prima specie. E siccome
possiamo aggiungere che la funzione è continua a sinistra di x=2.
2.
Studiare
la continuità della funzione
Il
punto a rischio di continuità è x=1 (punto di confine dei tratti).
Possiamo
osservare che
, dunque la funzione esiste nel punto x=1.
In
prossimità del punto si hanno i due seguenti limiti:
(primo tratto) e
(secondo tratto), dunque
.
Dunque x=1 è un punto di continuità e possiamo concludere che la funzione è sempre continua.
3.
Studiare la continuità della funzione
. La funzione è fratta e dunque in x=2 è discontinua. E’
conveniente eliminare il modulo trasformando la funzione come segue:
ovvero
Possiamo
osservare che
non esiste.
In
prossimità del punto si hanno i due seguenti limiti:
(primo tratto) e
(secondo tratto). Dunque x=2 è un punto di discontinuità
di prima specie. Ovviamente non esistendo
in questo caso non avremo
continuità parziale.
4.
Studiare la continuità della funzione
. 
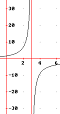
La
funzione è fratta e dunque in x=3 è discontinua.
non esiste e
. Si tratta di una discontinuità di seconda specie.
La
funzione presenta un asintoto verticale di equazione x=3.
5.
Studiare
la continuità della funzione
. La funzione è fratta e dunque in x=2 è discontinua.
non è calcolabile (si tratta di
una forma indeterminata 0/0). Invece
[1], dunque il limite esiste
ed è finito. Si tratta di una discontinuità di terza specie.
Tale discontinuità può essere eliminata ridefinendo la funzione nel seguente
modo:
; così facendo il valore assunto dalla funzione nel punto 2 (ovvero 4) è
uguale al valore cui tende al limite.
6.
Studiare
la continuità della funzione
. La funzione è fratta;
il denominatore si annulla nei
punti
e dunque ha due punti di
discontinuità.
In
x=+3 si ha
ovvero una discontinuità
di seconda specie:
la funzione ha un asintoto verticale di equazione x=3.
In
x=-3 si ha
[2]
ovvero una discontinuità di terza specie.
Tale discontinuità può essere eliminata ridefinendo la funzione nel seguente
modo:
; in tal modo rimane solo la discontinuità nel punto x=3.
7.
Studiare
la continuità della funzione
La funzione è definita a tratti e fratta; ci sono due punti di potenziale
discontinuità: x=3 e x=2.
Osserviamo
che x=3 non appartiene al tratto in cui la funzione fratta è
definita
e dunque non è un punto di
discontinuità.
La
funzione nel punto x=2 vale:
.
In
prossimità del punto si hanno i due seguenti limiti:
(primo tratto) e
(secondo tratto) ovvero :
.
La
funzione è dunque sempre continua.
Scarica il file zip
